p.171

1.


ここに（40+20）[kg]が掛かっている。

短い方にたくさん

∴Aのロープには36.67kgの荷重がかかる。 　　だから切れる。

---

2.

dm：dx部分の質量 dI：dx部分の慣性モーメント

半径＝(xsinq)と考えて、dI＝dm×(xsinq)²

全体の慣性モーメント＝

---

p.172

3.

重心は、中心線上にある。 see for reference p.145　図8.3 重心の位置をx3で表す。 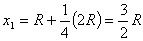m1＝円錐の質量 m2＝半球の質量

---

4.

---

5.

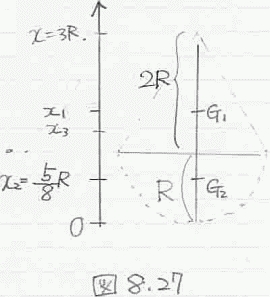Aが問題の図形．

線対称なのでAの重心は、線 l の上 にある。さらに、B, Cの重心は 各々の真ん中、OB, OCになることは明白。

各々の重さを、W_A，W_B，W_Cとする。
W_A＝pR²･r–pr²r
W_B＝pR²･r–2pr²r
W_C＝pr²r

O_Aを原点にして、l 上に座標を取る。Aの重心x_Gは
Bの重心とCの重心を足したもの。
∴W_A×x_G＝W_B×0＋W_C×(–S)
(pR²･r–pr²r)･x_G＝pr²r×(–S)
(R²–r²)x_G＝–S･r²

（答）	Rの円の中心から、rの円の中心へ向かって 進んだ位置

---

6.

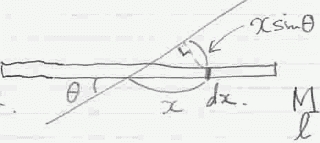
	棒を質点の集合体と 見なし、微小部分 drについて考える。
w：角速度
r：密度 dm：dr部分の質量 dK：dr部分の運動エネルギー v：dr部分の速度   v＝r･w	dm＝r･dr

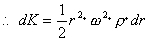
両辺を積分する，

M＝r･l より、

（答）

dL：dr部分の角運動量
一般に l ＝r×r＝r×mvより、
∴dL＝r×dm×rw＝r²･w･r･dr
   この両辺を積分する。

M＝r･l なので、

（答）

---

7.

	左図の様に、円柱を薄い 円板に分けて考える。 この部分の質量をdm、 密度をrとする。 ＝p･R2･ l ･r dm＝p･R2･dz･r
dIzG：薄い円板のzに関する慣性モーメント dIxG：薄い円板のxに関する慣性モーメント dIyG：薄い円板のyに関する慣性モーメント

・・・

教p.159

表8.1参照

直交軸の定理(p.159)より、dI_zG＝dI_xG＋dI_yG

対称性より   dIxG＝dIyG

重心から円板までの距離をZとして、x，y軸に関する
モーメントを、各々dI_x＝dI_yとして、
この式の両辺を積分する。


M＝pR²l r より

（答）

---

9.

☆棒の線密度を  として、棒の慣性モーメント I を求める。
M＝2 l ×r
dm＝r ･dx   ・・・微小部分dxの重さ
dI・・・dx部分の慣性モーメント
   

Ks：棒が鉛直線と角qを	なしている時	の運動エネルギー
	↓
	この時、棒の重心Gの位置 エネルギーの減少分を u とすれば

u＝Mg･l cos＝K_s

（答）